Mining GW Catalogs

Mining Gravitational Wave Catalogs To Understand Binary Stellar Evolution:
A New Hierarchical Bayesian Framework

Submitted to Physical Review D on June 21st, 2018.

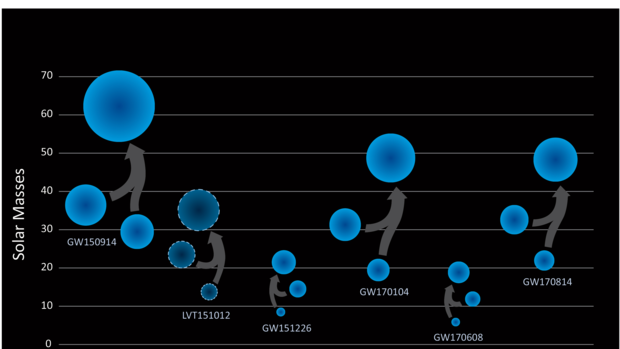
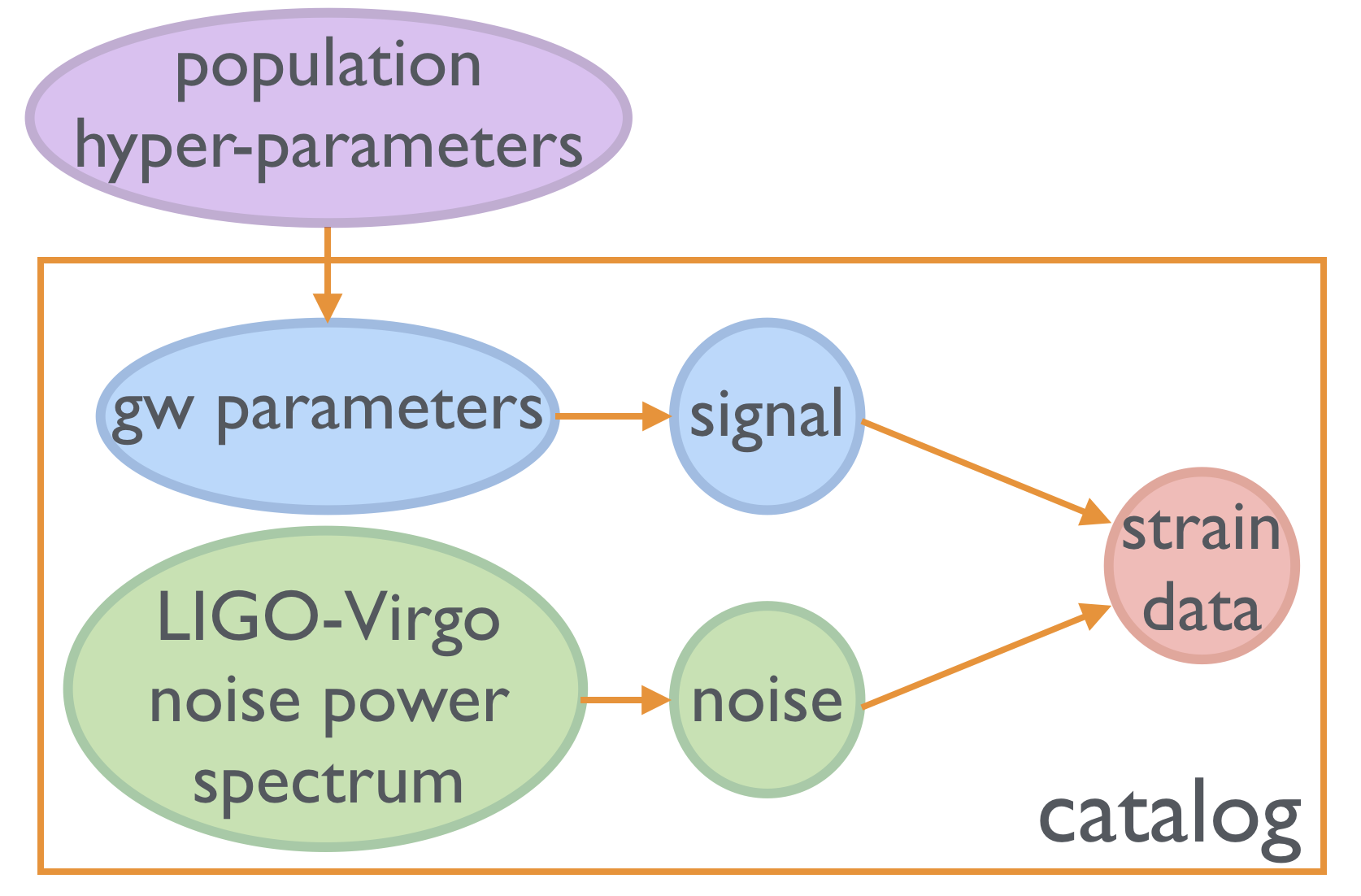
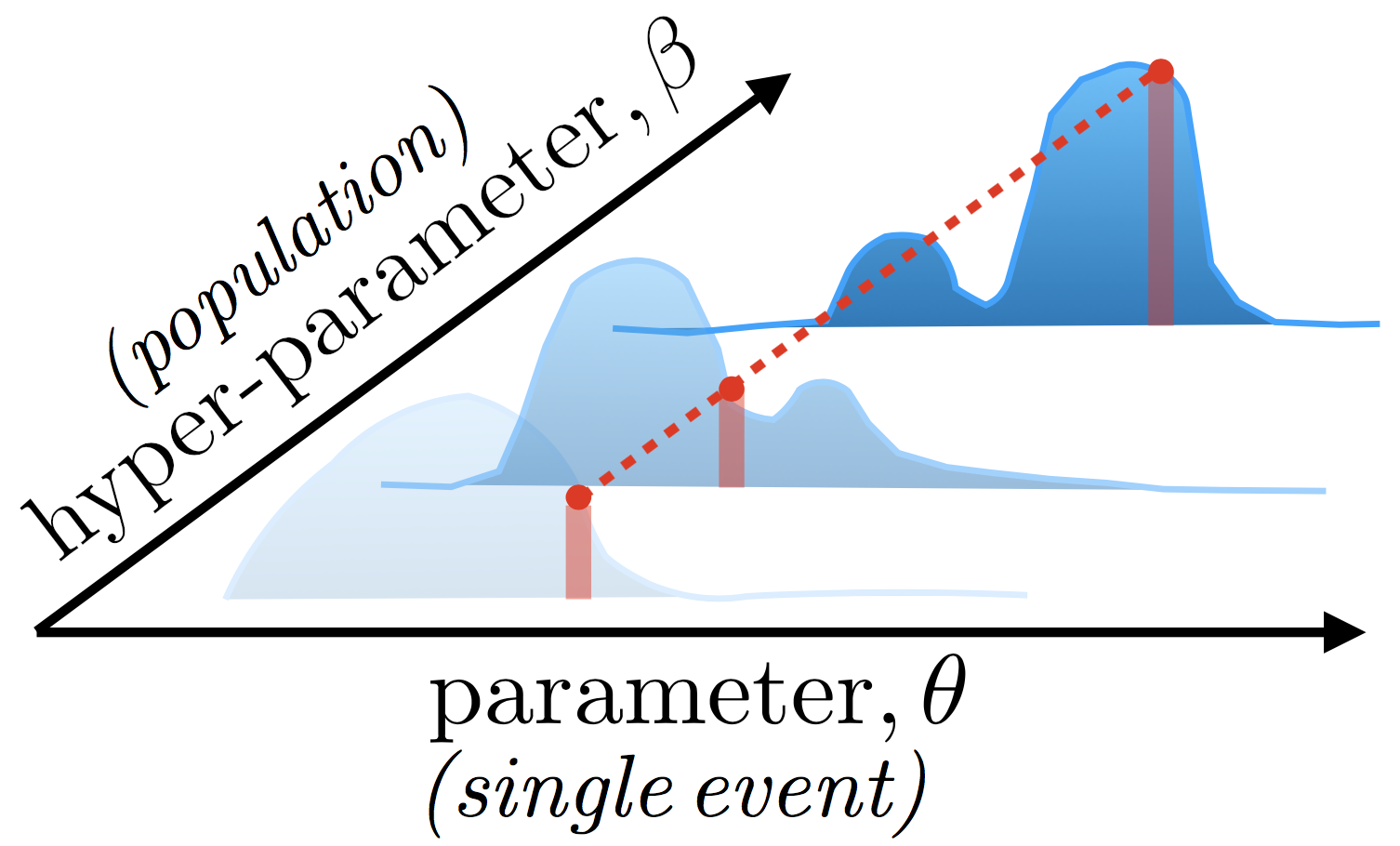
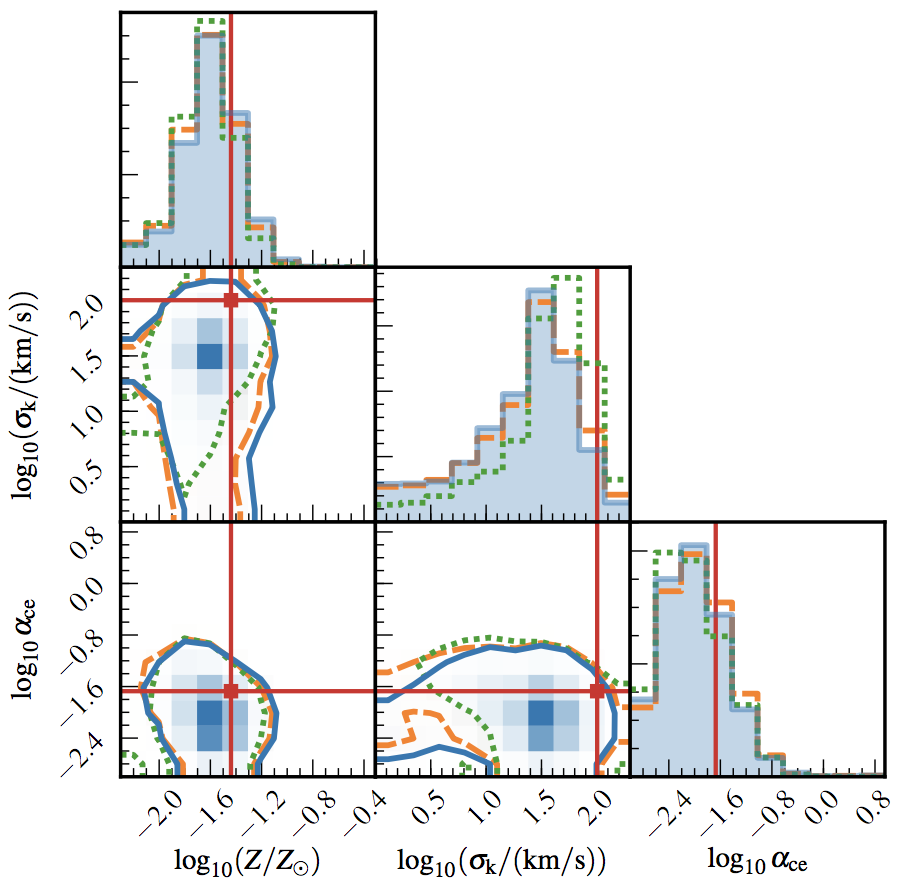
Catalogs of stellar-mass compact binary systems detected by ground-based gravitational-wave instruments (such as LIGO or Virgo) will offer insights into the demographics of progenitor systems and the physics guiding stellar evolution. The masses of existing binary black-hole detections already imply that the metallicity of their progenitor systems must have been sub-solar, and the combination of mass, redshift, spin, and rate information from future detections will further elucidate the underlying astrophysics. Existing techniques approach this through phenomenological models, discrete model selection, or model mixtures. Instead, we explore a technique that uses gravitational-wave catalogs to directly infer posterior probability distributions of progenitor metallicity, kick parameters, and common-envelope efficiency. We use a bank of compact-binary population synthesis simulations to train a Gaussian-process emulator that acts as a prior on observed parameter distributions (e.g. chirp mass, redshift, rate). This emulator slots into a hierarchical population inference framework to extract the underlying astrophysical origins of systems detected by LIGO, Virgo, etc. The method is fast, easily expanded with additional simulations, and can be adapted for training on arbitrary population synthesis codes, and detectors like LISA.

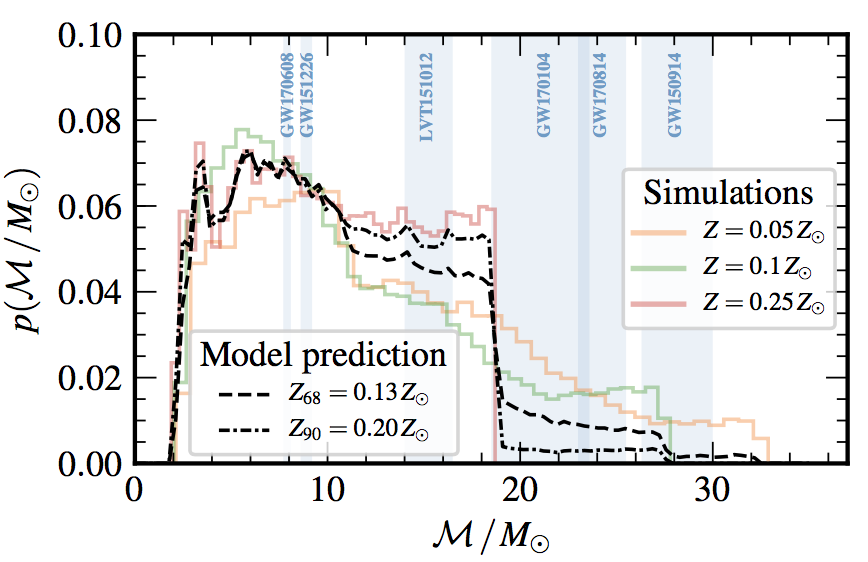
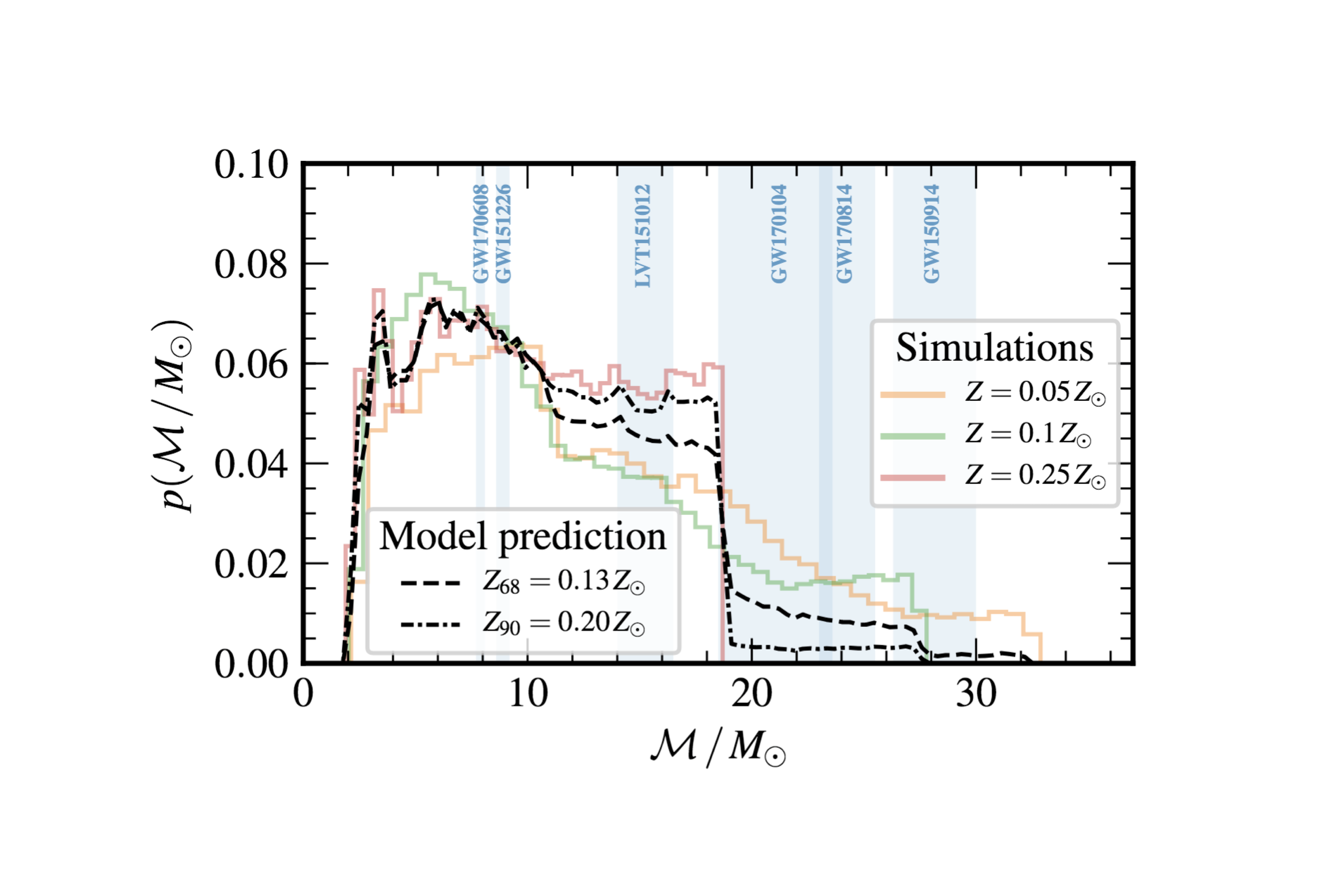Figure 1: Probability distribution of chirp masses for Stevenson et al. (2017) training simulations (colored lines) and our GP-emulator reconstructions (dashed and dash-dot lines).

Gravitational Wave Catalogs

Figure 2: Detected black-hole binaries [Credit: LSC/LIGO/Caltech/Sonoma State (Aurore Simonnet)]

The Advanced Laser Interferometer Gravitational-wave Observatory (aLIGO) has detected five binary black-hole (BBH) mergers and one double neutron star (DNS) merger since becoming operational in 2015, with Advanced Virgo (AdvVirgo) joining the hunt in August 2017.
Individual systems can teach us much, such as that BBH systems can form and merge within a Hubble time, and that their GW emission can be directly detected. We also learned that the emitted GW radiation was consistent with Einstein's General Relativity Theory. Likewise, the detection and electromagnetic follow-up of the DNS system (GW170817) showed that NS mergers could explain the origin of short gamma-ray bursts, gave insight into the equation-of-state of nuclear matter, constrained the graviton speed, and gave a measure of the Hubble constant.
The catalog of BBH mergers span a range of masses, distances, component spin-sky-locations, and sky-locations. One of the first surprising aspects of these systems is how massive they are, with the component BH masses in GW150914 being around 30 times as big as the Sun.
Attention is now turning to GW population inference, where we try to mine the catalog of detections to understand typical stellar evolutionary paths, progenitor conditions, and the fraction formed in the field versus dense stellar clusters.

Hierarchical Population Inference

Bayesian parameter estimation on a single GW event requires a choice of prior probabilities for the different intrinsic and extrinsic parameters. The prior on parameters such as component masses, spin magnitudes/orientation, source redshift, etc. should follow from our existing knowledge of the population. However, the standard safe-choice is for priors to be weak and un-informative (with broad ranges), so that the resulting posterior distributions are dominanted by data constraints.
In hierarchical population inference, we take the posterior samples from each event (usually from Markov Chain Monte Carlo analysis) and correct for the influence of this interim prior choice. This gets us back to the likelihood of each event. We can then multiply all of these likelihoods together, and constrain the entire cataloged population with a new prior.
This new prior may have its own population parameters, which are called hyper-parameters. These hyper-parameters can describe things like the shape of the chirp-mass distribution, the fraction of systems formed in the field versus in dense stellar clusters, the physical processes of stellar evolution, or progenitor star conditions.
The figure shown here is a probabilistic graphical model illustrating hierarchical population inference for LIGO. The signals will be gravitational-waveforms for each event, with waveforms having physical parameters which we constrain with a population prior. This population prior constrains "features" in parameter distributions determined from principal component analysis. The weights of these features (and thus the parameter priors) depend on hyper-parameters like progenitor metallicity, BH natal kick magnitude, and common-envelope hardening efficiency.

Figure 3: Example probabilistic graphical model for LIGO hierchical population inference.

Using Population Simulations To Train GW Parameter Priors

Figure 4: We perform population synthesis simulations of BBH systems initialized from different progenitor conditions and evolutionary assumptions. We interpolate the resulting parameter dsitributions as a function of these hyper-parameters to generate a new prior model for GW parameters.

Our approach to hierarchical population inference fuses agnostic modeling (i.e. measuring bin-heights in histograms of GW parameter distributions) with physically-detailed compact-binary population synthesis simulations.
We design a program of population simulations at different points in population hyper-parameter space. Each simulation produces a population of compact-binaries; we are interested mostly in BBH systems, but this can apply to any population or mixture of populations. These synthesized BBH systems are filtered for detectability in LIGO-Virgo, which will prefer closer and more massive systems.
We now have distributions of parameters of detectable BBH systems for different progenitor star conditions, evolutionary paths, etc. As illustrated here, we can interpolate the bin-heights (or pixel intensities) of these distributions across hyper-parameter space, allowing us to predict new distributions without performing more costly simulations. In practice, we use principal-compoennt analysis (PCA) to find characteristic "features" in these distributions, then interpolate over these features. This drastically reduces the number of interpolants that we need to train.
There are various choices of interpolation schemes that we could use, e.g. linear, spline, etc. We use Gaussian Process (GP) interpolation, which treats the data as a single random draw from a multi-variate Gaussian distribution. We can use the data to learn the structure of the correlation length-scales in hyper-parameter space. This allows us to interpolate and extrapolate. Crucially, we also gain a measure of the interpolation uncertainty, which we can include as additional sources of noise or uncertainty in our population analysis.

Mining Catalogs With A Trained Population Prior

Our interpolation over synthesized parameter distributions gives us an emulator of further simulation output. We have learned the connection between initial stellar population conditions and the distributions of measured GW parameters. We can now predict new parameter distributions and detection rates as a function of the physical processes guiding stellar evolution or dynamical formation scenarios.
In Figure 5 we trained on 3 publicly-available population simulations at different progenitor metallicities. Our GP emulator could then predict chirp-mass distirbutions at different metallicites. In a simple analysis of the current LIGO-Virgo catalog, we found that systems preferred a 90% upper limit of ~20% solar metallicity. The figure shows the reconstructed intrinsic chirp-mass distribution implied by different metallicity constraints.
For the analysis in Figure 6, we trained our GP interpolants using a custom program of 125 simulations across progenitor metallicity, BH natal kick magnitude, and common-envelope hardening efficiency. Lower metallicity allows stars to remain more massive throughout their evolution, resulting in more massive BHs. This seems to be needed to produce the massive BHs seen in LIGO's current catalog.

Figure 5: The different color lines show the intrinsic chirp-mass distribution from three publicly-available population simulations at different progenitor metallicities. The black dashed and dotted lines show GP model reconstructions at metallicities from a simple analysis of the current LIGO-Virgo catalog.

Figure 6: Marginalized posterior probability distribution of population hyper-parameters for a mock catalog of 100 BBH systems. The true hyper-parmeters are indicated via red lines.

For Figure 6, we tested our GP emulator within a full hierarchical Bayesian pipeline, where we analyzed a catalog of 100 BBH systems from a simulation that was not included in the training process.

In blue we used distribution and rate information (marginalizing over poorly-constrained scaling factors) to constrain the population, whereas in orange we only used distribution information. Green used a variant of the distribution and rate approach. In all cases our Bayesian probability distirbutions were completely consistent with the true population conditions.

Authors

Dr. Stephen R. Taylor

Dr. Davide Gerosa